1. 介绍

走迷宫是一个比较经典的算法问题，它既可以使用广度优先算法，也可以使用深度优先算法，这2种算法的本质是不一样的。

广度优先算法:周围每个点都走一下，周围的点走往后，前往下一个点继续周围的点走一下，以此类推。都是点到为止，不多走，这样可以保证达到终点时，路径一定是最短的。不需要使用到递归。

深度优先算法:从一个点，一直走到底，走到不能走。需使用递归实现。

本文使用广度优先算法实现查找迷宫最短路径。

2. 需求

使用文件内规定好的迷宫，0是通路，1是阻碍，迷宫从起点走到终点。并且在走完后，可以告知能否到达终点以及具体路径。

迷宫

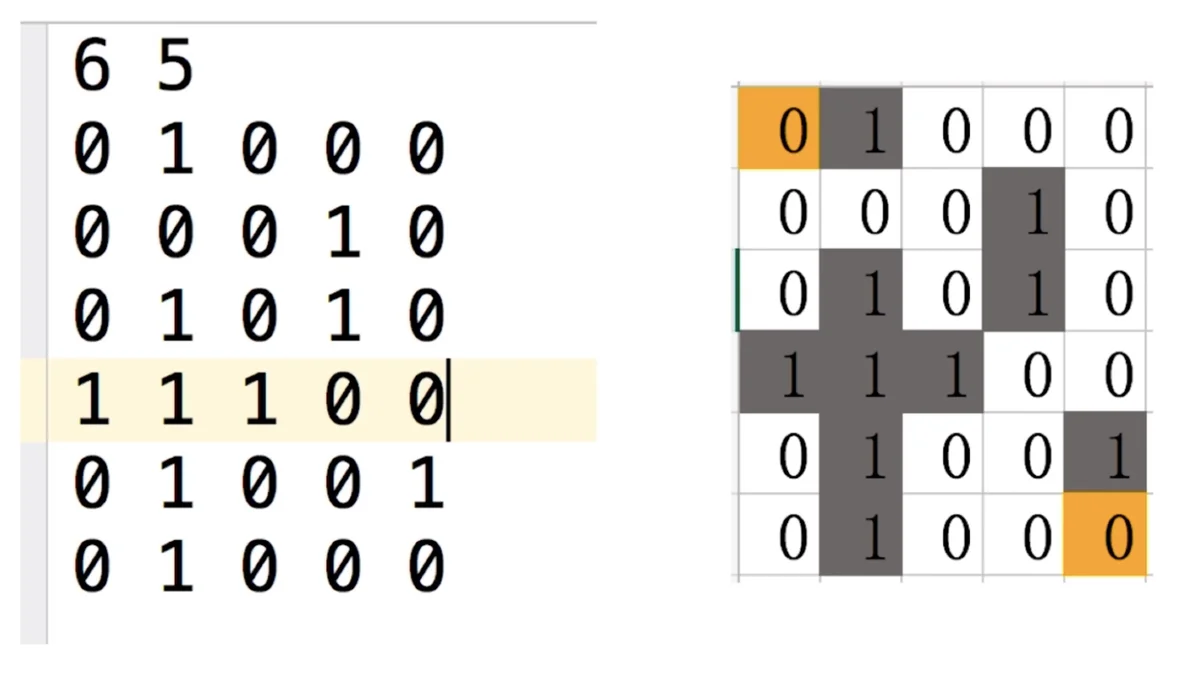
maze_init

3. 思路分析

1.首先，需要先定义探索的方向顺序，我们将其排序为先上后左再下最后右。

走完后需要先退回来再走左边而不是继续顺着再往下探索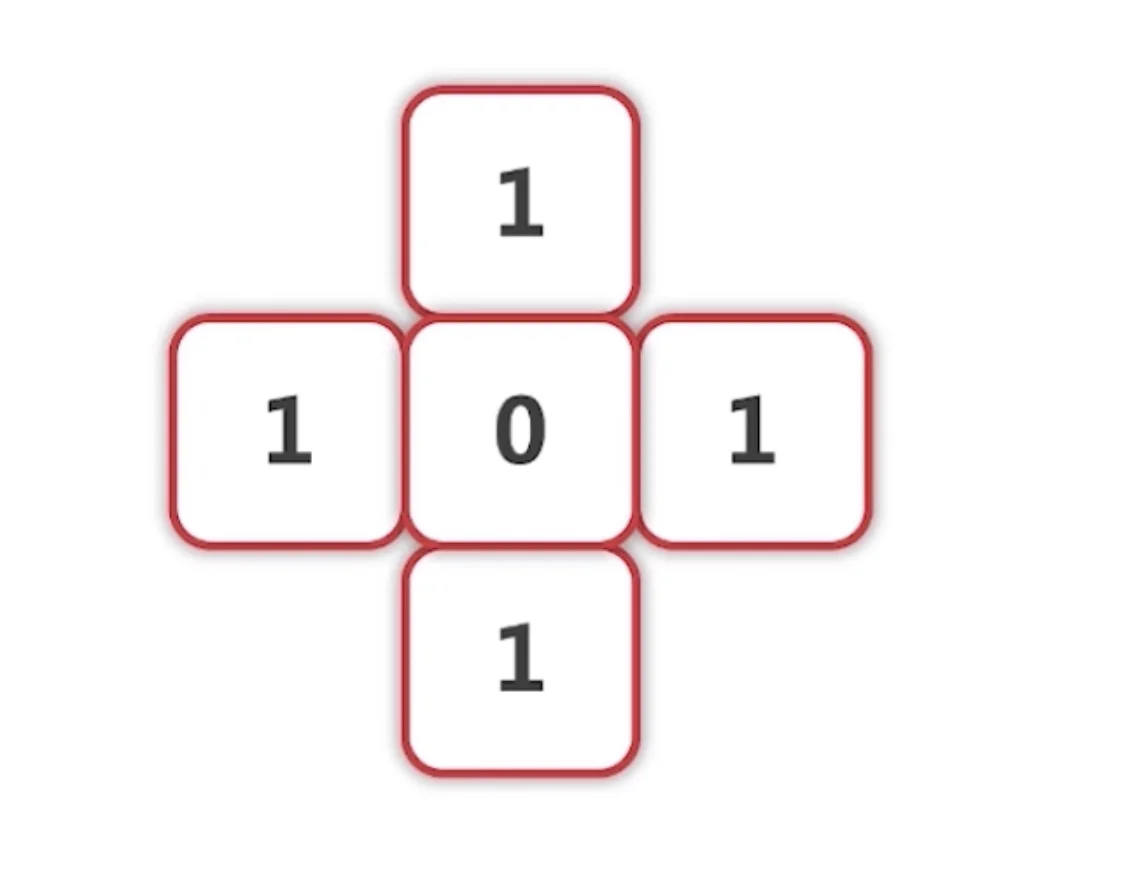

maze_first

3.周围四个点技术后，我们再前进一个点，继续按照2的步骤进行探索，以此类推。

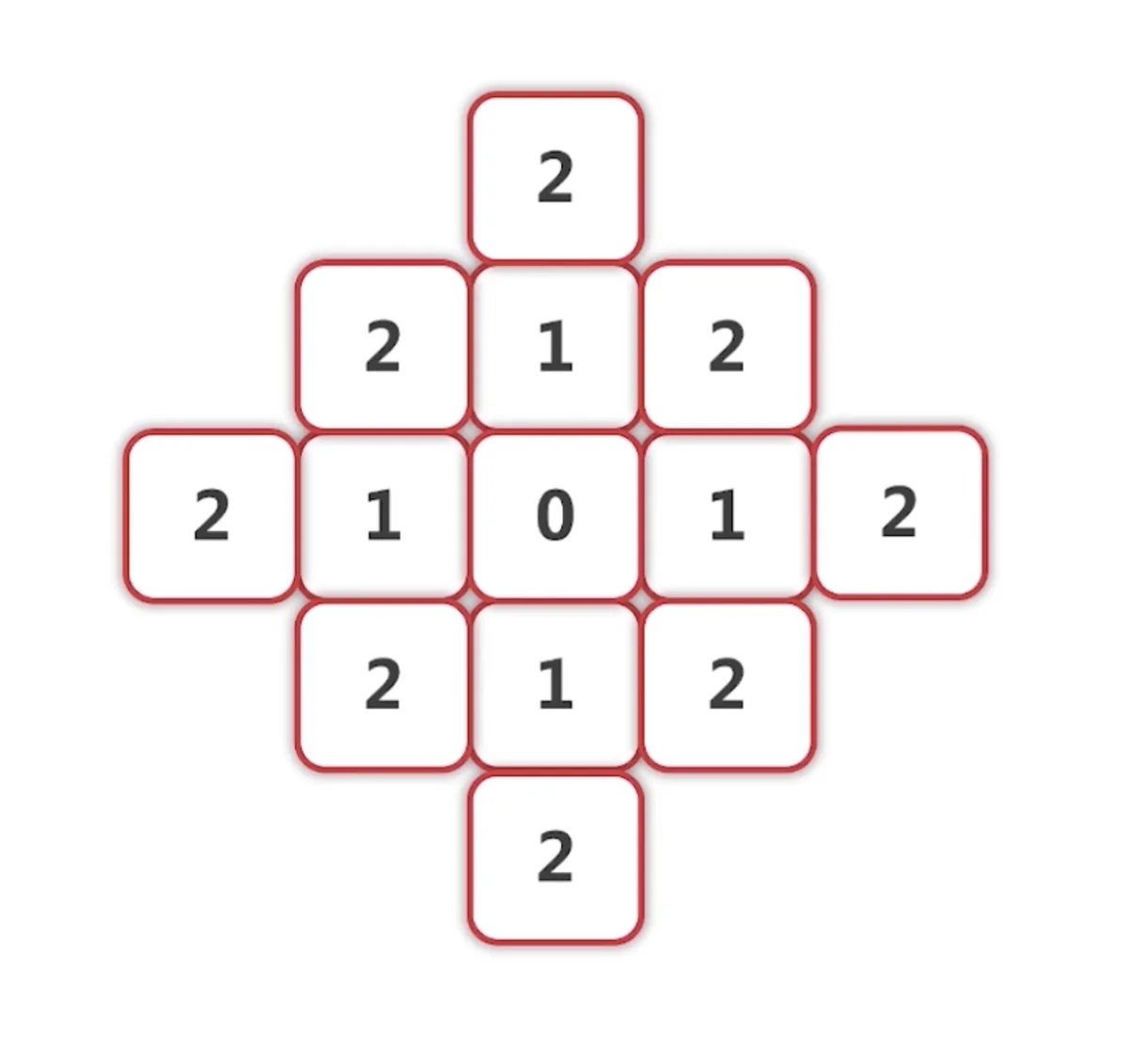
maze_second

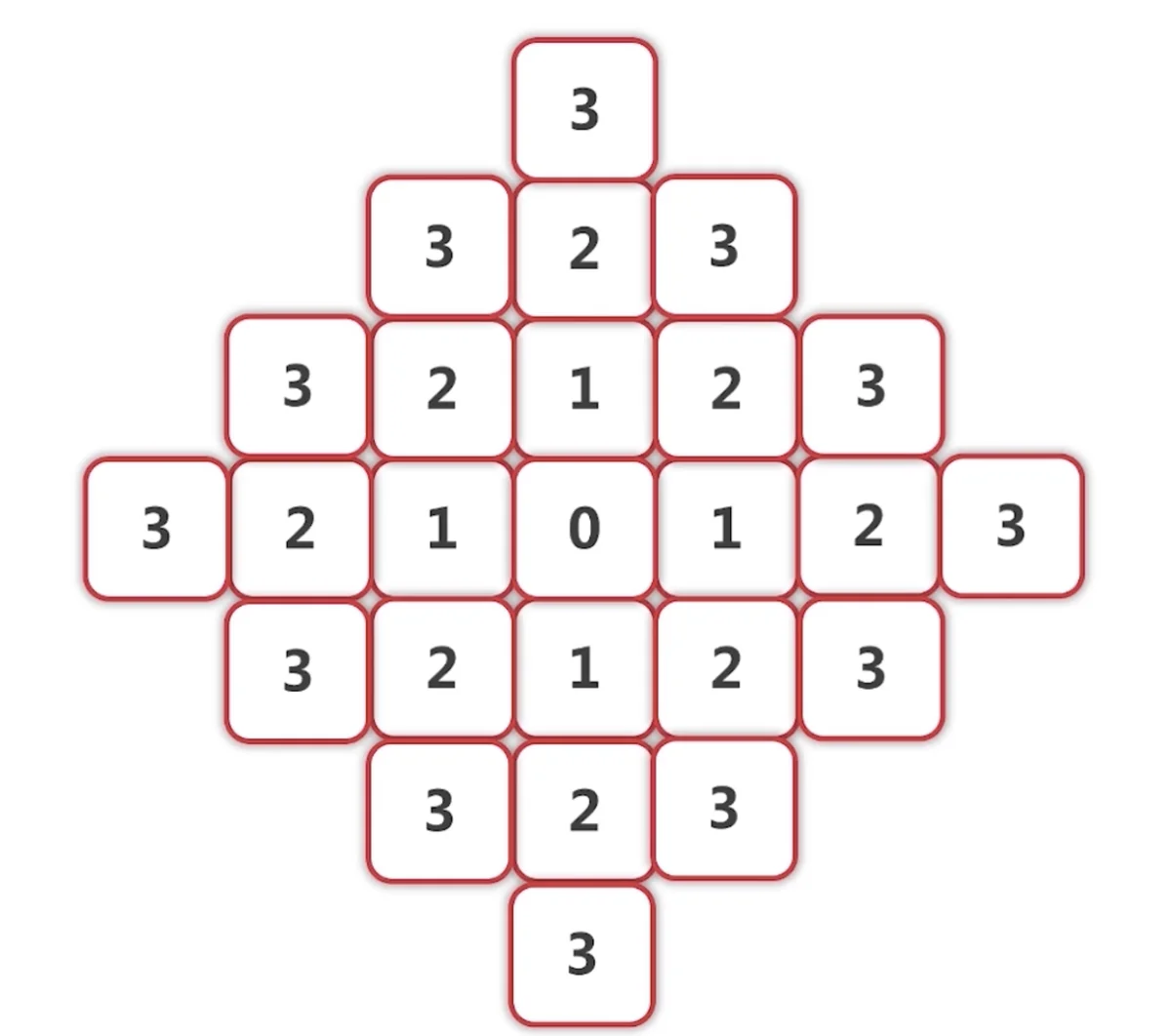
maze_third

4.这样，当我们碰到终点时，路径一定会是最短的。

4. 算法分析

1.首先，我们需要做一个队列，可以使用切片来模拟。这个队列用来存放可以探测的点，然后每次都从这个队列将点取出，进行4个方向的探测，每一个可以探测的点，都再存放到这个队列里。

(1,0)(1,0)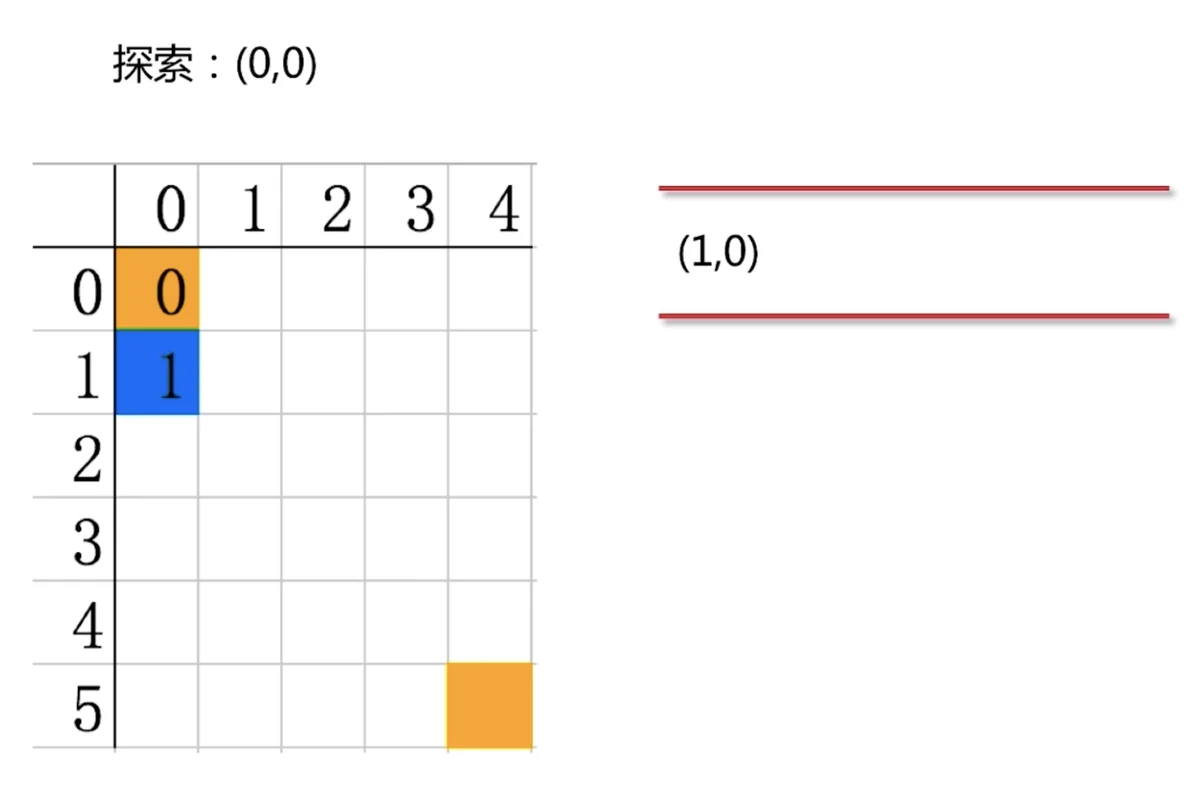

maze_queue

(1,0)(2,0)(1,1)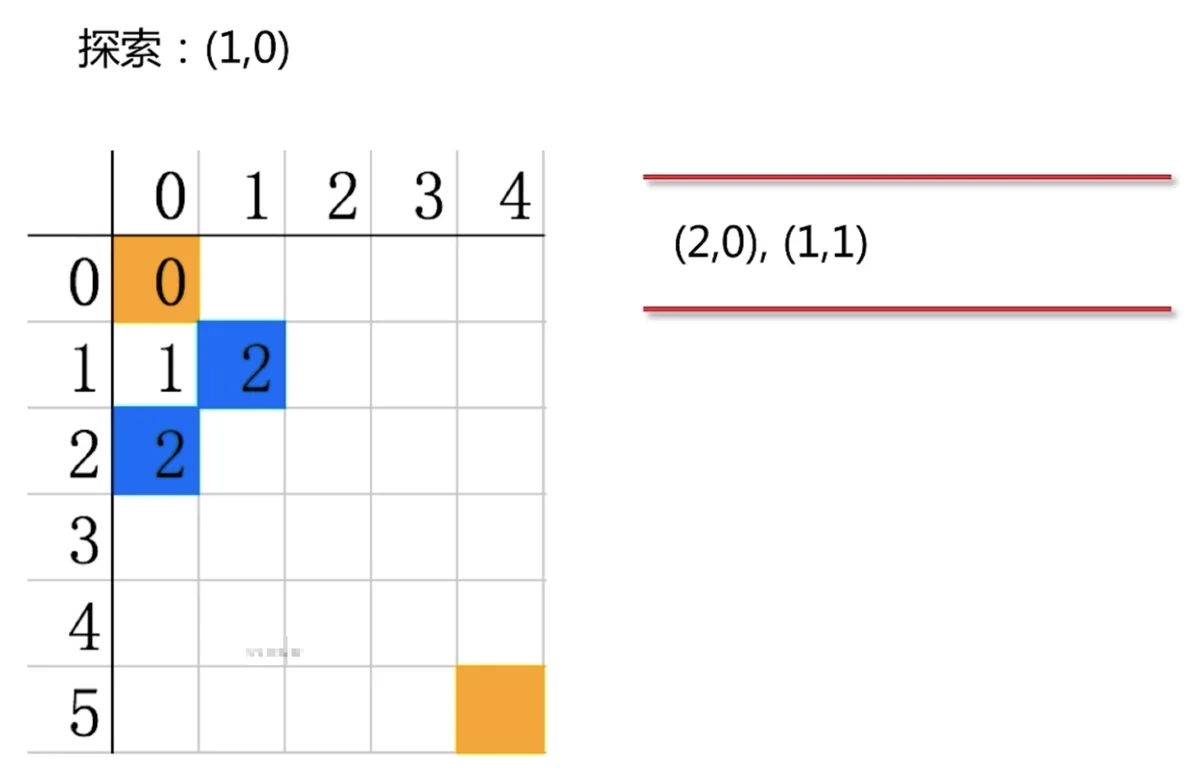

maze_queue1

(1,2)(0,2)(1,1)(2,2)(1,1)(0,2)(2,2)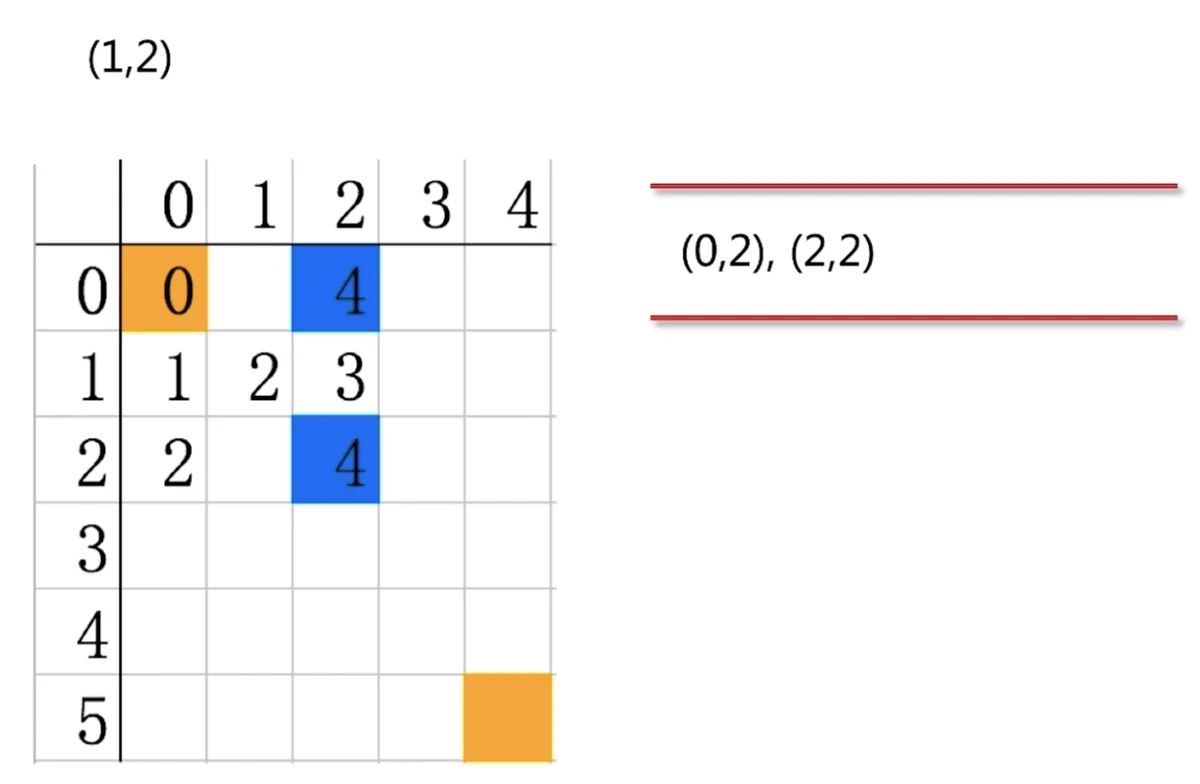

maze_queue2

5.最后，当探测的点等于终点时，证明迷宫可以走出。所以，我们还需要另一张地图，专门用来记录走的路径以及第几步。

5. 最终结果

以上面的地图为例，最终我们会获得这样一个二维数组。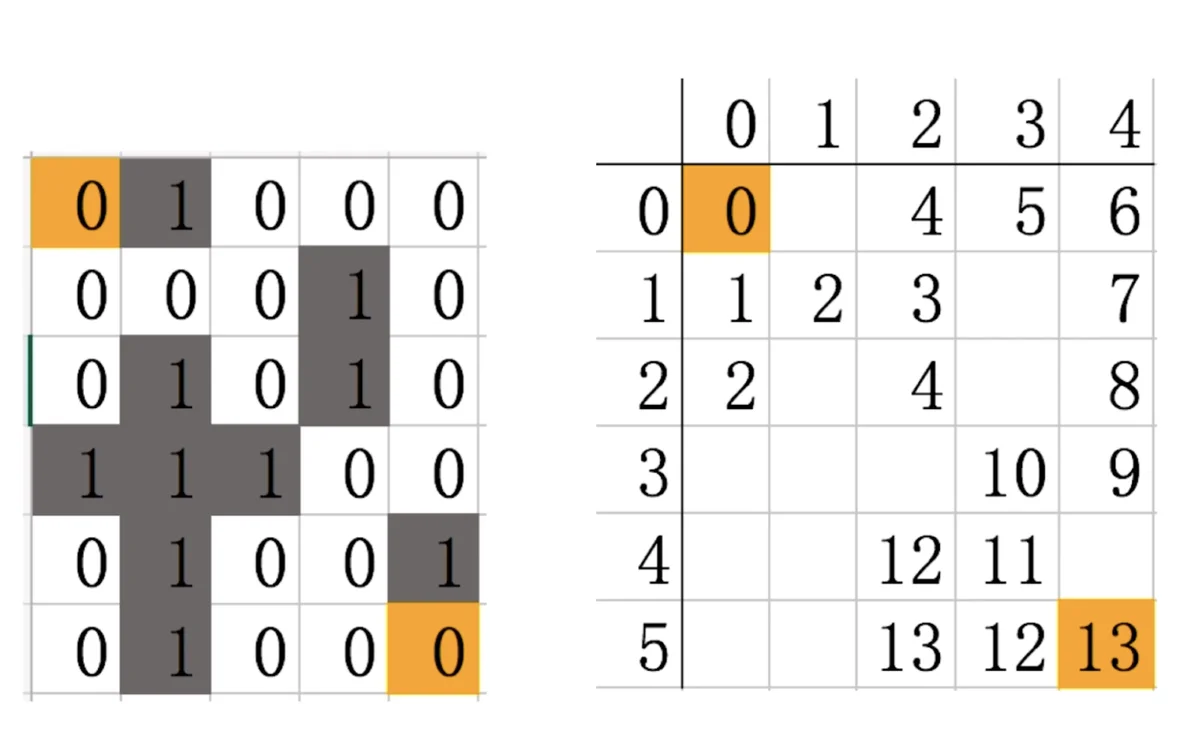
maze_end

那应该如何找到走过的路径？从终点开始，往回走，比如此时终点是13，那么就找12的点在哪。然后把终点替换为12，再去找11在哪里，以此类推，最终找到0，就找到了整个迷宫所走的路径。

6. 代码实现
maze.ini
1
2
3
4
5
6
7
6 5
0 1 0 0 0
0 0 0 1 0
0 1 0 1 0
1 1 1 0 0
0 1 0 0 1
0 1 0 0 0

maze.go

point
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
package main

import (
	"fmt"
	"os"
)

//从配置文件中读取行，列，以及地图规则
func getMap(row, col *int) [][]int {

	file, err := os.Open("./maze.ini")
	if err != nil {
		panic(err)
	}
	fmt.Fscanf(file, "%d %d", row, col)
	maze := make([][]int, *row)
	for i, _ := range maze {
		maze[i] = make([]int, *col)
		for j, _ := range maze[i] {
			fmt.Fscanf(file, "%d", &maze[i][j])
		}
	}
	return maze
}

//构建二维切片
func getTwoSlice(row, col int) [][]int {
	two_slice := make([][]int, row)
	for i, _ := range two_slice {
		two_slice[i] = make([]int, col)
	}
	return two_slice
}

//定义坐标类型，不过坐标类型需要依照二维数组下标的规则
type point struct {
	i, j int
}

//上 左 下 右 四个方向
var directions = [4]point{
	{-1, 0},
	{0, -1},
	{1, 0},
	{0, 1},
}

//计算点计算后的结果
func (this point) addPoint(dir point) point {
	//故意不设置为引用传递，这样不需要重新创建一个point返回
	this.i += dir.i
	this.j += dir.j
	return this
}

//判断该点是否越界以及返回该点的值为多少
func (this *point) normalGetValue(myMap [][]int) (int, bool) {
	//先比行
	if this.i < 0 || this.i >= len(myMap) {
		return -1, false
	}

	//再比列
	if this.j < 0 || this.j >= len(myMap[0]) {
		return -1, false
	}

	//返回具体的值
	return myMap[this.i][this.j], true
}

//打印地图
func printMap(myMap [][]int) {
	fmt.Println("开始打印地图:")
	for _, value := range myMap {
		for _, val := range value {
			fmt.Printf("%d\t", val)
		}
		fmt.Println()
	}
}

//判断地图是否找到终点
func findEndPointAndPath(myMap [][]int, end point) ([]point, bool) {
	var queue []point
	end_value := myMap[end.i][end.j]
	if end_value == 0 {
		//证明没有到达重点
		return queue, false
	}
	//如果找到了,先将终点存入切片
	queue = append(queue, end)
	for {
		if end_value < 0 {
			//如果比0小，证明已经全找完了。
			break
		}
		//此时end_value的值是我们想要找的值
		end_value--
		for _, dir := range directions {
			//继续寻找周围符合的点
			next := end.addPoint(dir)
			//再判断该点是否会越界
			data, ok := next.normalGetValue(myMap)
			if !ok || data != end_value {
				continue
			}
			//通过证明是我们要找的点，存到切片中
			queue = append(queue, next)
			//更换end点
			end = next
			break
		}
	}
	return queue, true
}

//开始执行，传入地图以及当前步数地图。开始位置以及终点位置
func walk(maze, steps [][]int, start, end point) [][]int {
	//1. 先将起点放入队列
	queue := []point{start}
	for {
		if len(queue) == 0 {
			//如果队列取完了，证明已经结束了，退出程序
			break
		}
		//没有走完，就取出队列第一个数，进行判断。
		first := queue[0]
		queue = queue[1:]

		for _, dir := range directions {
			//运算后，计算出下个点的坐标
			next := first.addPoint(dir)

			if next == end {
				//证明这个运算后的点就是重点了
				//此时在步数地图进行记录，然后退出
				steps[next.i][next.j] = steps[first.i][first.j] + 1
				break
			}

			//判断该点是否符合要求
			//前提，都需要该点没有越界

			//1.判断在maze地图中是否为1，1是墙就跳过
			res, ok := next.normalGetValue(maze)
			if !ok || res == 1 {
				continue
			}

			//2.判断在steps地图中是否已经走过了，已经走过证明不通或者别的点会走，直接跳过
			res, ok = next.normalGetValue(steps)
			if !ok || res != 0 {
				continue
			}
			//3.判断是不是起点，如果是起点就跳过
			if next == start {
				continue
			}
			//如果全部通过，证明可以走
			//把这个点加入队列，可以继续探测
			//并且将步数进行记录
			queue = append(queue, next)
			steps[next.i][next.j] = steps[first.i][first.j] + 1

		}
	}
	//将步数地图返回
	return steps
}

func main() {
	var row, col int
	maze := getMap(&row, &col)
	printMap(maze)
	steps := getTwoSlice(row, col)
	start := point{0, 0}
	end := point{5, 4}
	res := walk(maze, steps, start, end)
	printMap(res)

	path, ok := findEndPointAndPath(steps, end)
	if ok {
		fmt.Println("最短路径坐标:")
        for i := len(path) - 1; i >= 0; i-- {
			fmt.Printf("%v ", path[i])
		}
	} else {
		fmt.Println("对不起，没有找到通往终点的路径")
	}
}
7. 运行结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
开始打印地图:
0	1	0	0	0
0	0	0	1	0
0	1	0	1	0
1	1	1	0	0
0	1	0	0	1
0	1	0	0	0
开始打印地图:
0	0	4	5	6
1	2	3	0	7
2	0	4	0	8
0	0	0	10	9
0	0	12	11	0
0	0	13	12	13
最短路径坐标:
{0 0} {1 0} {1 1} {1 2} {0 2} {0 3} {0 4} {1 4} {2 4} {3 4} {3 3} {4 3} {5 3} {5 4}