[算法]剑指offer p20顺时针打印矩阵 golang 题目

题目：输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。例如：如果输入如下矩阵

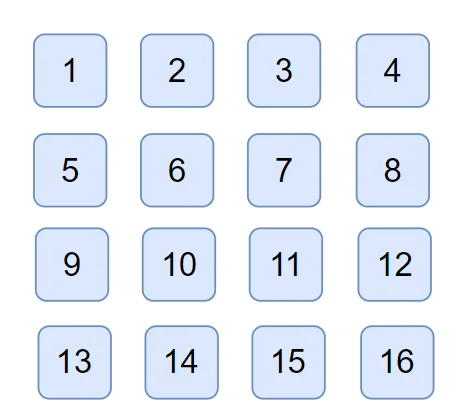
image-20220214191643765

输出的顺序为

{1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 15} 解法1

对于复杂代码的设计, 一般都要再编写之前讲清楚思路和设计

看起来这个题目没有涉及到任何的数据结构, 但是各种边界情况却比较复杂,我们要再编写之前将将思路讲清楚, 通过示例找到规律

一圈一圈打印

我们可以用一个循环来打印每次打印矩阵的一个圈

每个圈的上右下左(top,right,bottom,left) 依次打印

如图: 绿色是第一圈, 橘色是第二圈

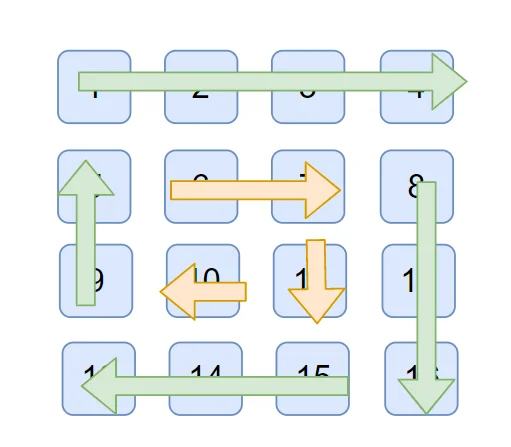
image-20220214192149303

结束条件

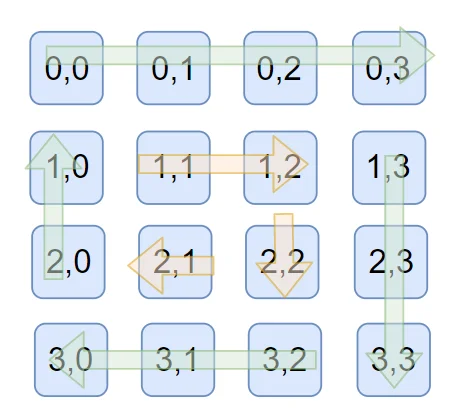
image-20220214194311231

将矩形展示位坐标如上图所示, 第一圈的的起点是 (0,0) 第二圈的起点是 (1,1)

将起点记为 start(第一圈 start = 0 第二圈 start = 1)

columnMax为列树的最大下标这里为 3

rowMax为行数的最大下标这里为 3

top: 上边的坐标移动为 (start,start) -> (columnMax - start,start)right: 右边坐标移动为(start+1,columnMax-start) -> (rowMax-start, columnMax-start)bottom: 下边坐标移动为(rowMax-start,columnMax-start-1) -> (rowMax-start, start) (逆向减少 i–)left: 下边坐标移动为(rowMax-start-1,start) -> (start+1, start) (逆向减少 i–)

那么, 结束条件是什么呢?

我们可以发现上边任何一条边无法打印了就会结束

上边: start * 2 fmt.Printf("%s\n", "err: matrix is empty") return } //用这个圈控制范围和结束 start := 0 rowMax := len(matrix) - 1 columnMax := len(matrix[0]) - 1 for { //打印上边 if start*2 except = append(except, matrix[start][i]) } } else { break } //打印右边 if start+1 break } //打印右边 if start+1 except = append(except, matrix[i][columnMax-start]) } } else { break } //打印下边 if columnMax-start-1 >= start { for i := columnMax - start - 1; i >= start; i-- { except = append(except, matrix[rowMax-start][i]) } } else { break } //打印左边 if rowMax-start-1 >= start+1 { for i := rowMax - start - 1; i >= start+1; i-- { except = append(except, matrix[i][start]) } } else { break } start++ } return except } 单元测试 func TestP20(t *testing.T) { examples := []struct { matrix [][]int except []int }{ { matrix: [][]int{ {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}, }, except: []int{1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10}, }, { matrix: [][]int{ {1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, }, except: []int{1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7}, }, { matrix: [][]int{ {1, 2, 3, 4}, {5, 6, 7, 8}, }, except: []int{1, 2, 3, 4, 8, 7, 6, 5}, }, { matrix: [][]int{ {1, 2, 3, 4}, }, except: []int{1, 2, 3, 4}, }, { matrix: [][]int{}, except: []int{}, }, } for _, e := range examples { actual := clockWiseMatrix(e.matrix) assert.Equal(t, e.except, actual) fmt.Printf("actual: %v\n", actual) } }

debug

actual: [1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10] actual: [1 2 3 4 8 12 11 10 9 5 6 7] actual: [1 2 3 4 8 7 6 5] actual: [1 2 3 4] err: matrix is empty actual: [] PASS