leetcode之94二叉树的中序遍历Golang

题目描述

root

示例 1：

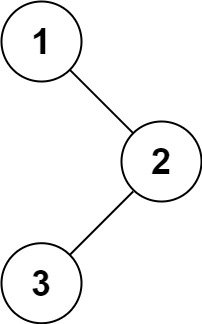
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

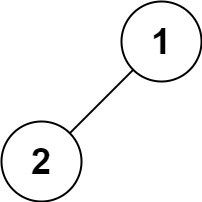
输入：root = [1,2]
输出：[2,1]

示例 5：

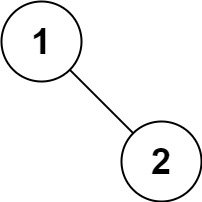
输入：root = [1,null,2]
输出：[1,2]

提示：

[0, 100]-100 <= Node.val <= 100

算法

如果采用递归的方式中序遍历二叉树，那么将会很简单，所以我们在这里采用迭代的方式中序遍历二叉树，在这里我们需要用到的数据结构是栈

go

算法核心思想如下：

• 首先将二叉树的根结点入栈
• 判断栈顶的结点的左子树是否已经遍历完毕
  • 已经遍历完毕：那么将栈顶结点的值保存到结果数组中，并且将栈顶结点弹出栈中，然后将该结点的右子树的根结点压入栈中
  • 没有遍历完毕：那么将不将栈顶结点出栈，并且将栈顶结点的左子树的根结点压入栈中
• 当栈重新变为空栈的时候，整棵二叉树就已经遍历完成了

代码如下：

func inorderTraversal(root *TreeNode) []int {
	// 中序遍历的顺序是左中右
	// 本算法采用迭代的方法完成，采用的核心工具是栈
	resArr := make([]int, 0)
	if root == nil {
		return resArr
	}
	stack := []*TreeNode{root}
	flag := false
	for len(stack) != 0 {
		if flag {
			rightChild := stack[len(stack)-1].Right
			resArr = append(resArr, stack[len(stack)-1].Val)
			stack = stack[:len(stack)-1]
			// 说明有右子树，所以将右子树的根结点入栈
			if rightChild != nil {
				stack = append(stack, rightChild)
				// 重新初始化标志，表示该根节点的左子树还没有遍历完
				flag = false
			}
			continue
		}
		leftChild := stack[len(stack)-1].Left
		if leftChild != nil {
			stack = append(stack, leftChild)
			continue
		}
		// 左子树为空，说明左子树已经遍历完毕
		flag = true
	}
	return resArr
}