Python3排序算法04

1. 算法介绍

希尔排序（Shell Sort）递减增量排序算法（diminishing increment sort）插入排序希尔排序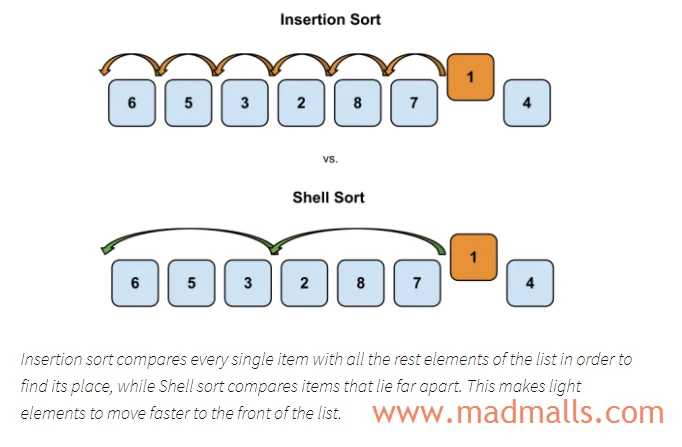

算法的主要步骤如下：

步长

gap = 4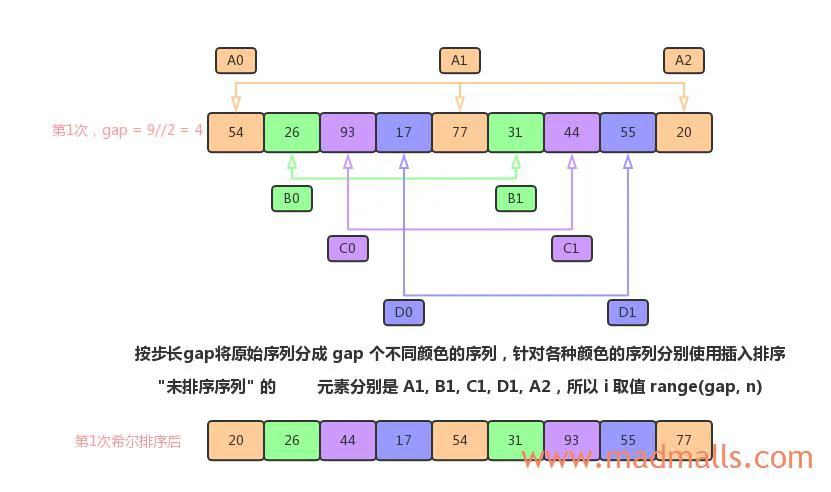

gap = 2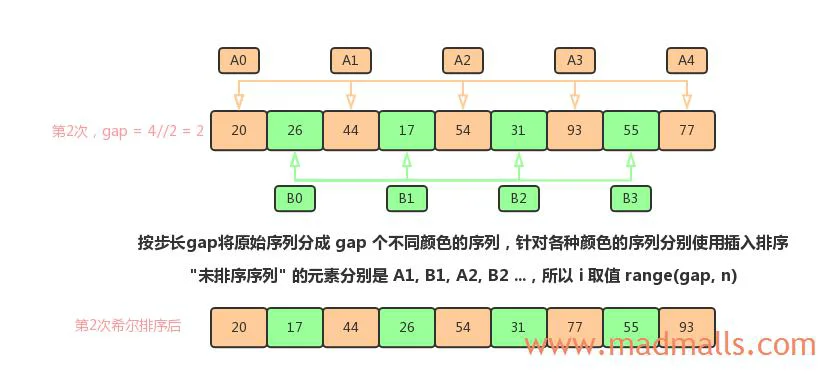

gap = 1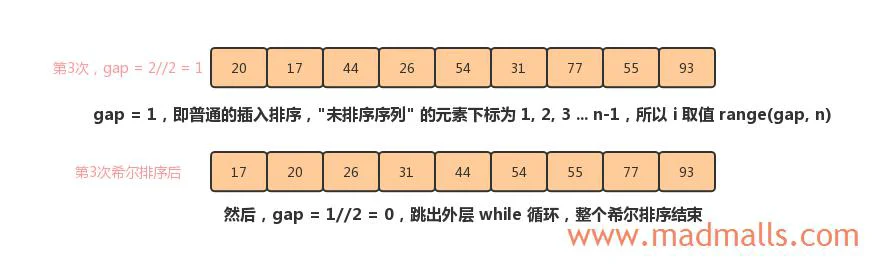

2. Python实现

步长

2.1 算法1

步长n / 2

def shell_sort(L):
    '''希尔排序，升序'''
    n = len(L)
    if n <= 1:
        return

    gap = n // 2  # 初始步长
    while gap > 0:  # 最后一次步长为1（即普通的插入排序），然后整个希尔排序结束

        # 想像成，以步长 gap 将原始序列划分成 gap 个待排序的序列，对每个序列使用普通的插入排序进行排序
        # 序列1: [L[0], L[gap], L[2*gap]...]
        # 序列2: [L[1], L[1+gap], L[1 + 2*gap]...]
        # 序列3: [L[2], L[2+gap], L[2 + 2*gap]...]
        # 请查看插入排序算法 https://github.com/wangy8961/python3-algorithms/blob/master/4.%20%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F%20-%20Insertion%20Sort/3_best_insertion_sort_asc.py
        # 助记：普通的插入排序算法中步长是 1 ，把插入排序中的步长 1 替换为 gap
        for i in range(gap, n):  # "未排序序列" 的第1个元素分别是L[gap], L[1+gap], L[2+gap] ... ，所以变量 i 表示的下标是 gap, 1+gap, 2+gap ...
            temp = L[i]
            j = i
            # j >= gap是因为后续j[j-gap]，否则下标越界
            while j >= gap and temp < L[j-gap]:
                L[j] = L[j-gap]
                j -= gap
            L[j] = temp

        gap = gap // 2  # 得到新的步长


if __name__ == '__main__':
    L1 = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print('Before: ', L1)
    shell_sort(L1)
    print('After: ', L1)

    # Output:
    # Before:  [54, 26, 93, 17, 77, 31, 44, 55, 20]
    # After:  [17, 20, 26, 31, 44, 54, 55, 77, 93]

压力测试：

from timeit import timeit


def shell_sort():
    # import random
    # gen = (random.randint(1, 100) for i in range(100))  # 产生100个 1-99 范围内的随机整数
    # L = list(gen)
    L = [96, 2, 65, 23, 47, 58, 8, 48, 69, 92, 34, 83, 93, 47, 45, 55, 95, 15, 92, 24, 64, 19, 29, 55, 35, 48, 39, 29, 63, 94, 99, 38, 50, 10, 10, 93, 74, 27, 74, 44, 29, 81, 85, 86, 74, 30, 50, 50, 12, 12, 38, 75, 41, 87, 80,