切片 append 是比较常规的操作,但存在一个隐患,当初始cap设置的比较小,而实际要存储的元素非常多时,性能损耗就会比较突出。比如下面这个例子,当 for 循环的次数足够多时,就会触发到性能瓶颈
func main() {
elems := make([]string, 0)
for i := 0; i < 1000; i++ {
elems = append(elems, strings.Repeat("跑马灯 ", 100))
}
}
基于这个例子,我们用单测来验证一下,在单测中保存 cpu profile 数据到文件 cpu.p中,在开始执行测试之前,使用 ResetTimer重置时间,取消创建文件的性能开销
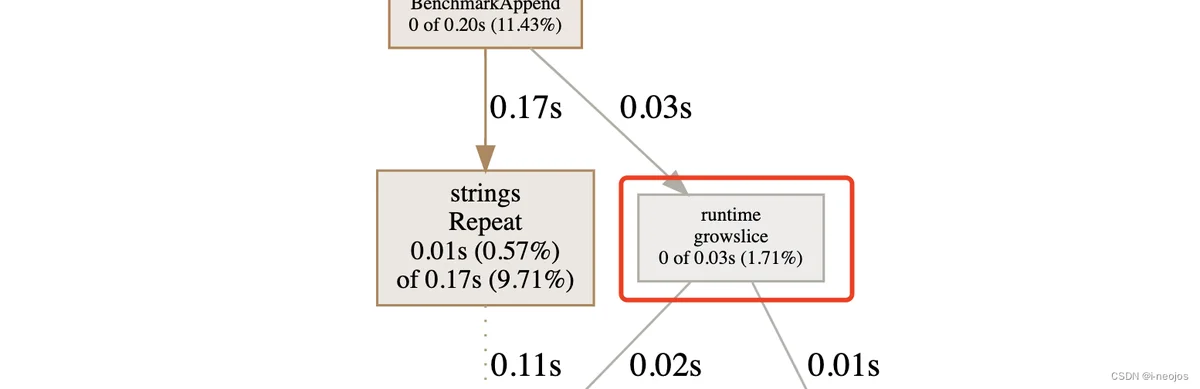
下面是分析的结果,我们把焦点集中在 growslice上,这个单测有点缺陷,就是每次 for 循环都会调用一次 string.Repeat 函数,导致 Repeat 函数的 cpu 消耗反客为主了。但不重要,能说明问题。
但很多时候,我们对这个功能点不够重视,业务中经常也会写一些没有声明 cap 容量的变量声明,然后直接调用 append,逻辑上是没有问题的,只有当 append 的数量足够多的时候,性能问题才会突出来了。
live := make([]BigObject, 0) // 缺少声明cap
live = append(live, BigObject{})
在初始化切片时设置了cap为2,但实际上元素有600个,这时切片容量的增长就称为了一个性能的损耗点。这种情况,底层会按照2倍的扩容方式,2、4、8、16…,总共会扩容9次,每次扩容过程,旧数据内存都会拷贝到新数据的空间。
这种2倍的增长模式,也不是固定的,具体的增长算法,依赖我们预期(这里我叫 eCap,expect capacity)的值,当达到阈值1024,会采用两种不同的增长策略。
引申一个想法
如果初始化切片设置的cap比较小,实际要存储的元素个数也比较小,我们如何评估影响呢?这让我联想到了时间复杂度,时间复杂度评估的就是耗时和数据量N的关系,关注的是一种变化,而非某个具体的N是多少。
所以,创建切片的时候,合理地预估容量非常重要。slice底层的切片扩容机制这里简单说明一下:
扩容的参考依据有两个,当前切片的容量,这里称为 oCap(old capacity)。满足当前切片需求的最小容量,这里称为 eCap。当 oCap 小于 1024时,按照 2 倍 oCap进行扩容,当容量大于 1024时,按照 1/4 oCap的容量增长,这里的 1/4 是具有叠加效应的。我们来实现一下伪代码,假设新的切片容量为 nCap:
if oCap < 1024 {
nCap = 2 * oCap
} else {
nCap = oCap
for oCap < eCap {
nCap = 1/4 * nCap + nCap
}
}
对比的看一下 go1.18 下的源代码:
对比一下上面我自己想的伪代码,有一些考虑不完善的地方。
- 缺少了 eCap 和2倍 oCap 容量的比较逻辑
- oCap值可能是负值,这回导致伪代码的 for 循环变成死循环
newcap := old.cap
doublecap := newcap + newcap
if cap > doublecap {
newcap = cap
} else {
const threshold = 256
if old.cap < threshold {
newcap = doublecap
} else {
// Check 0 < newcap to detect overflow
// and prevent an infinite loop.
for 0 < newcap && newcap < cap {
// Transition from growing 2x for small slices
// to growing 1.25x for large slices. This formula
// gives a smooth-ish transition between the two.
newcap += (newcap + 3*threshold) / 4
}
// Set newcap to the requested cap when
// the newcap calculation overflowed.
if newcap <= 0 {
newcap = cap
}
}
}
切片的扩容逻辑比较简单,也没有什么高深的地方。留一个思考题,指定 slice 中的一个下标,将下标前的部分和下标后的部分颠倒?
